Chi-Square Distribution

 Chi-Square Distribution:

• Definition: The Chi-Square Distribution is a continuous probability distribution that arises in statistics. It is commonly used to model the distribution of the sum of the squares of $k$ independent standard normal random variables, where $k$ is known as the degrees of freedom ($df$). It's denoted as ${\chi }^2(df)$.

• 
  

  Probability Density Function (PDF): The PDF of the Chi-Square Distribution is defined as:

  $f(x;k)=\frac{1}{2^{k\mathrm{/}2}\cdot \mathrm{\Gamma }(k\mathrm{/}2)}\cdot x^{(k\mathrm{/}2)-1}\cdot e^{-x\mathrm{/}2}$

  Where:

  • $x$ is the random variable.
  • $k$ is the degrees of freedom.
  • $\mathrm{\Gamma }(k\mathrm{/}2)$ is the gamma function evaluated at $\frac{k}{2}$.

• 
  

  Mean and Variance: The mean of the Chi-Square Distribution is $k$, and the variance is $2k$.

• 
  

  Graphical Representation:

  Here's a probability density function (PDF) plot of the Chi-Square Distribution for various degrees of freedom ($k$):

  

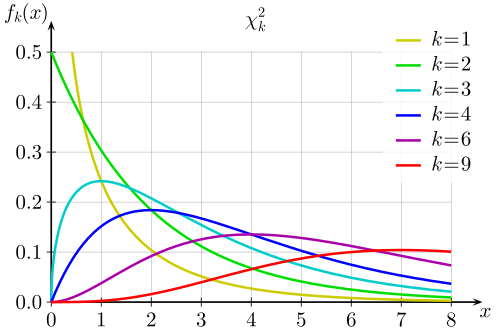
  In this graph, you can see the PDF for different values of $k$. As $k$ increases, the Chi-Square Distribution becomes more symmetric and approaches a normal distribution.

• 
  

  Use Cases:

  • Hypothesis Testing: The Chi-Square Distribution is commonly used in hypothesis testing, especially in tests of independence and goodness of fit.
  • Confidence Intervals: It is used to construct confidence intervals for population variances.
  • Statistical Inference: The Chi-Square test statistic is used to determine if observed data fits an expected distribution.

The Chi-Square Distribution plays a crucial role in various statistical tests and is fundamental in the field of inferential statistics. It is particularly useful when dealing with categorical data and making inferences about population variances.